[MST] kruskal(크루스칼), prim(프림) 알고리즘

Programming/Data Structure

[MST] kruskal(크루스칼), prim(프림) 알고리즘

code_wizard 2024. 2. 16. 23:16

# 신장트리(Spanning Tree)

신장(spanning): 간선의 갯수를 가장 작게 노드를 전부 이어라.(= n-1개)

n개 정점
n-1개의 노드

# 최소 신장트리(MST: Minimum Spanning Tree)

네트워크에 있는 모든 정점들을 가장 적은 수의 (간선 + 비용)으로 연결

최소: 비용을 가장 작게

신장: 최소한의 간선으로(= n-1개)

=> 즉 최소신장트리는 싸이클이 없다.

<신장트리 vs 최소신장트리>

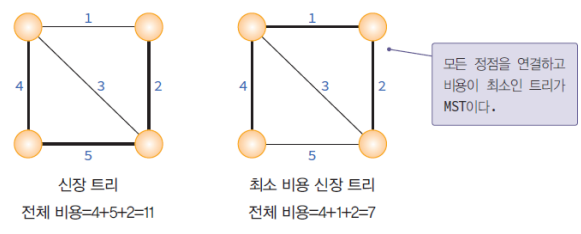
# 크루스칼 알고리즘

<사전지식>

그리디: 전체적인 해답을 찾는다는 희망으로 매 순간 최선의 선택을 하는 것.

과연 근데 그게 궁극적으로 최선인 걸까?

ex)

네비지도를 보고 가다가 잠시 빠른 길로 간 게

뒤에가 다 막히는 길이여서 더 늦을 수 있음.

=> 따라서 매 순간 최선의 선택이 최적의 해답임을 보장할 수 없음.

<크루스칼 수학적 그리디 증명>

그런데 크루스칼은 수학적으로 그리디가 최적의 해답임이 증명됨. (pass)

<크루스칼 알고리즘 순서>

1. 간선들 가중치로 오름차순 정렬

2. 하나씩 edge로 추가

3. 싸이클 발생하면 안됨, 싸이클 발생정점은 버린다.

4. 그다음 작은 거 선택

5. 무한반복

<그림풀이>

=> 싸이클 발생하면 제거.

<union-find를 이용해서 구현>

union: 결합동작(A, B를 합집합 한다.)

find: 싸이클이 있는지 검사(= 같은 부모에서 왔니?)

find는 부모를 찾아주는 거임(부모 같으면 같은 집합 == 싸이클 생긴다는 뜻)

넣으려고 했더니 한 몸통이면 안되는 거임(다른 집합 이어야 함.)

다른 몸통이어야 싸이클이 발생 안 함.

같은 집합이 아닐 때만, union 실행.

<코드레벨 알고리즘>

자기의 부모를 가리키고 있음.

배열이름: parent, 부모의 정보를 담고 있는 배열

=> while로 끝까지 가서 -1이 나오면 부모임. 부모를 return

<둘의 부모가 다르면>

싸이클이 생기지 않는다. union실행.

집합 1의 집합 2가 자식으로 들어간다.

# 크루스칼 시간복잡도: O(Elog(E))

대부분 간선들을 정렬하는 시간에 좌우됨.

※싸이클 검사는 정렬보다 훨씬 작은 오버헤드

따라서 시간복잡도 간선 E일 때, O(Elog(E)) 최적의 정렬만큼 시간복잡도 걸림.

# prim 알고리즘

현재 갈 수 있는 애들 중 가장 최적의 길을 택함.

<코드>

INF = float('INF')
def prim(n, costs, x):
    selected = [False]*n # 우리편
    distance = [INF]*n # 가중치를 담는 배열  
    adj_mat = [[INF]*n for _ in range(n)] # 인접행렬
    
    # 1)graph init 
    for c in costs:
        adj_mat[c[0]][c[1]] = adj_mat[c[1]][c[0]] = c[2] # 가중치
 
    distance[x] = 0 # 초기화    
    # 2) 비즈니스 로직
    for i in range(n): 
        # distance의 최솟값 찾기
        minnum = [0, INF]
        for idx, value in enumerate(distance):
            if not selected[idx] and value < minnum[1]:
                minnum[0] = idx # 인덱스
                minnum[1] = value # 값
                
        selected[minnum[0]] = True # 우리편으로
        # if distance[minnum[0]] == INF: return
        for idx, value in enumerate(adj_mat[minnum[0]]):
            if adj_mat[minnum[0]][idx] != INF:
                if not selected[idx] and value < distance[idx]: 
                    distance[idx] = value # 최솟값으로 업데이트 
    
    print(distance)
    return sum(distance)

def solution(n, costs):
    result = prim(n, costs, 0) # 아무데서나 시작, # 모든 가중치 더하면, 가장 적은 비용으로 통행하는 가중치
    return result

=> 배열로 구현했지만 heapq가 더 빠름.

prim은 인접행렬을 사용하면 o(v^2)
우선순위 큐를 사용하면 O((V + E)logV)