
https://www.acmicpc.net/problem/22968
22968번: 균형
이진 탐색 트리의 한 종류인 AVL Tree는 "높이 균형 성질"이라는 성질을 이용해 트리의 균형을 맞춘다. 또한, 높이 균형 성질을 만족하는 이진 탐색 트리는 전부 AVL Tree이다. 트리 $T$의 모든 내부
www.acmicpc.net
문제
이진 탐색 트리의 한 종류인 AVL Tree는 "높이 균형 성질"이라는 성질을 이용해 트리의 균형을 맞춘다.
또한, 높이 균형 성질을 만족하는 이진 탐색 트리는 전부 AVL Tree이다.
트리 의 모든 내부 정점 에 대해, 의 왼쪽 부트리와 오른쪽 부트리의 높이 차이가 1 이하일 때, 는 높이 균형 성질을 만족한다고 부른다.

위 그림에서, 왼쪽에 있는 트리는 모든 내부 정점의 왼쪽 부트리와 오른쪽 부트리의 높이가 동일하므로 AVL Tree이다.
가운데에 있는 트리는 5, 6, 8번 정점의 왼쪽 부트리와 오른쪽 부트리의 높이 차이는 1, 나머지 정점들은 0이므로 AVL Tree이다.
오른쪽에 있는 트리는 8번 정점의 왼쪽 부트리와 오른쪽 부트리의 높이 차이가 2이므로 AVL Tree가 아니다.
양의 정수 가 주어지면, 최대 개의 정점을 사용해서 만들 수 있는 AVL Tree의 최대 높이를 출력하는 프로그램을 작성하자.
입력
첫째 줄에 테스트 케이스의 개수 가 주어진다.
둘째 줄부터 개의 줄에 걸쳐 정점의 개수 가 한 줄에 하나씩 주어진다.
출력
총 개의 줄에 걸쳐 정답을 출력한다.
각 테스트 케이스마다, 최대 개의 정점으로 만들 수 있는 AVL Tree의 최대 높이를 출력한다.
제한
- 1 ≤
- 1 ≤

| 예제 입력1 |
| 5 1 2 5 10 1000000000 |
코드
from sys import stdin
r_line = stdin.readline
num = int(r_line())
n_1 = 4
n_2 = 2
h = 3
ans = [0]*num
for i in range(int(num)):
n = int(r_line())
if n < 3:
ans[i] = n
else:
temp = n_1 + n_2 + 1
while(temp <= n):
n_2 = n_1
n_1 = temp
h += 1
temp = n_1 + n_2 + 1
#print("temp", temp, "h", h)
ans[i] = h
h = 3
n_1 = 4
n_2 = 2
for i in range(num):
print(ans[i])풀이
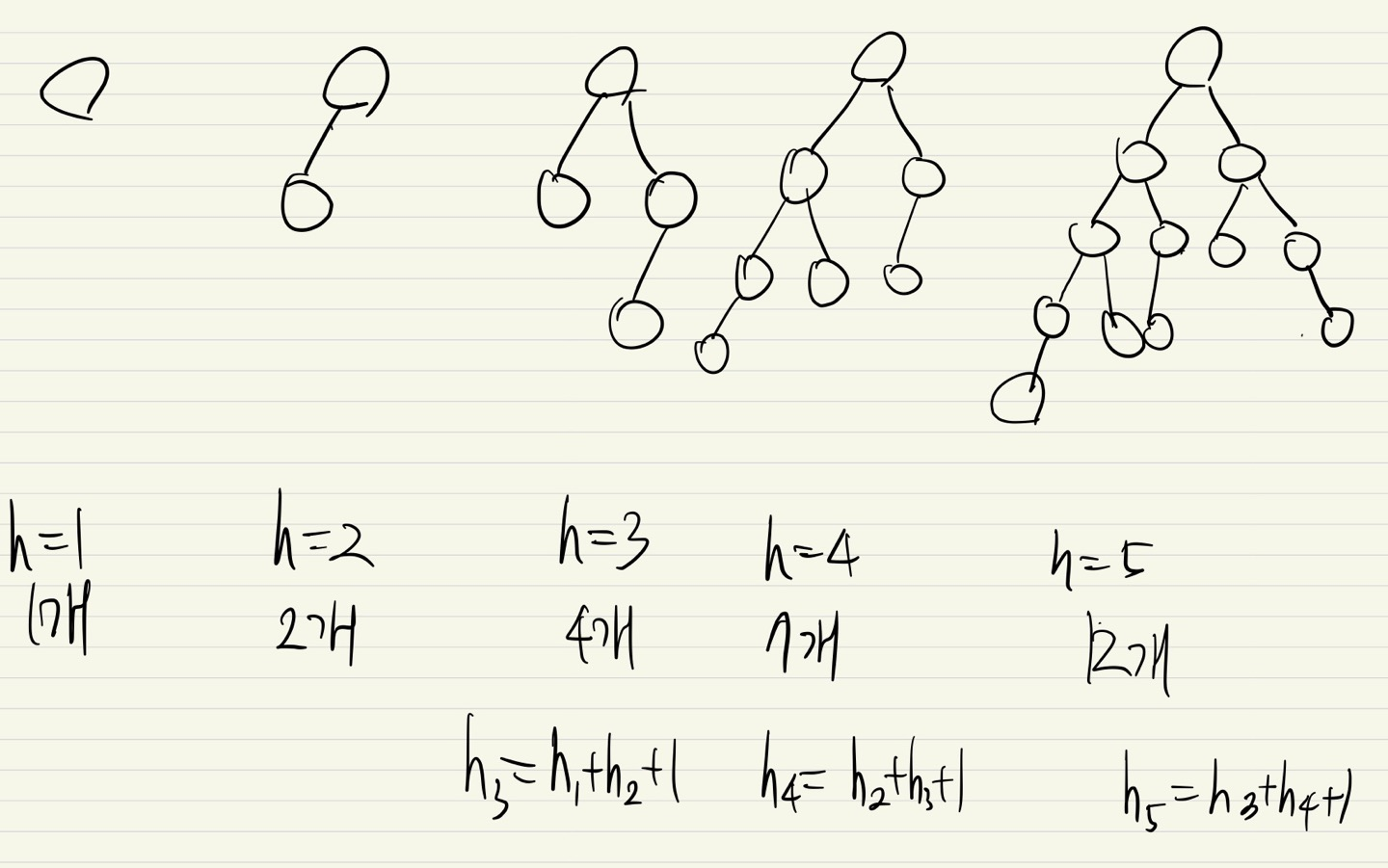
avl의 트리개념을 공부한 적이 있어서, avl트리를 트리의 개념적으로 먼저 접근했었다.
하지만 생각대로 답이 나오지 않았다.
이유는 개념으로 푸는 문제가 아닌, dp로 bottom-up방식의 점화식을 찾는 게 핵심이었다.
이처럼 작은문제에서 큰 문제를 해결하는 문제는 문제를 해결하려 하지 말고
작은 문제부터 차근차근 접근해야 한다.
점화식은
n = (n-1) + (n-2) + 1
이 나오게 된다.
'Programming > Algorithm(Python)' 카테고리의 다른 글
| [백준/python][dp] 백준 13703번 - 물벼룩의 생존확률 (0) | 2023.09.01 |
|---|---|
| [백준/python][브루트포스] 백준 1018번 - 체스판 다시 칠하기 (0) | 2023.09.01 |
| [백준/python][그래프] 2606번 - 바이러스 (0) | 2023.09.01 |
| [백준/python][그리디] 20115번 - 에너지 드링크 (0) | 2023.09.01 |
| [백준/python][구현] 21966번 - (중략) (0) | 2023.09.01 |
