우선순위 큐
- 우선순위를 가진 항목들을 저장하는 큐
- 우리가 정한 우선순위대로 정해진 큐
원래라면 1차선 도로처럼 FIFO 순서대로 나아가는 것을 큐(Queue)다.
2차선처럼 우선순위가 높은 데이터가 먼저 나가는 것이 우선순위 큐다.
숫자의 크기를 가지고 일단 우선순위 큐를 만들어보자.
우선순위 큐(heap)은 2가지로 구분
- 최소 우선순위 큐 (min heap)
- 최대 우선순위 큐(max heap)
우선순위 큐 구현방법
3가지가 존재한다
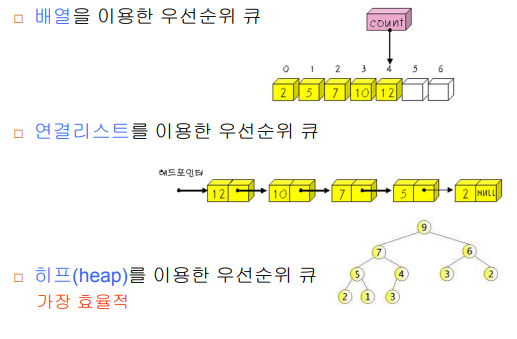
1. 배열을 이용한 우선 순위 큐
| 정렬이 안된 배열 | 정렬이 된 배열 |
삽입 - O(1)
|
삽입 - O(n)
|
연결리스트는 배열과 비슷하다.
3. Heap을 이용한 우선순위 큐
heap이란 무엇인가 하면

이런 뭉텅이를 의미한다.
무슨말이냐면, 정렬이 완전하게 되는 게 아니라
적당히, 이렇게 모여서 모아둔거마냥 반만 정렬되어 있는 상태를 의미한다.
따라서 heap은
노드들이 저장하고 있는 키들이 다음과 같은 식을 만족하는 완전 이진트리(complete binary tree)
1. max heap
부모 노드의 키값이 자식 노드의 키값보다 크거나 같은 완전 이진트리 ( 쉽게 말해, 부모가 큼)
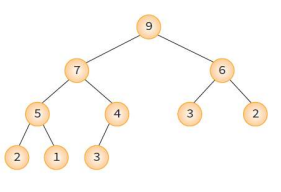
2. min heap
부모 노드의 키값이 자식 노드의 키값보다 작거나 같은 완전 이진트리 ( 쉽게 말해, 부모가 작음)
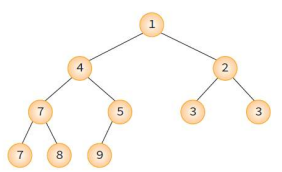
heap의 높이 log₂n
heap은 구현할 때
배열을 이용하여 구현한다.
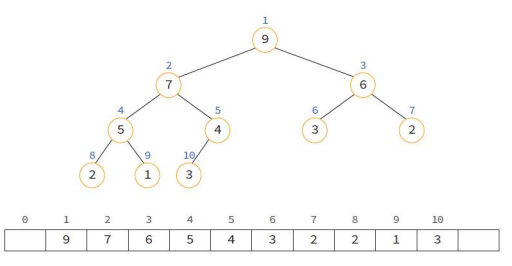
배열의 index를 heap의 번호라고 생각한다.
배열로 만들었을 때 장점은
=> 부모노드와 자식노드를 찾기가 쉽다.(관계식이 있기 때문)
- 왼쪽 자식의 인덱스 = (부모의 인덱스)*2
- 오른쪽 자식의 인덱스 = (부모의 인덱스)*2 + 1
- 부모의 인덱스 = (자식의 인덱스)/2
무조건 /2 하면 부모노드의 인덱스를 알 수 있다.
*2 + 1을 하면 오른쪽 자식의 인덱스를 알 수 있다.
이처럼 관계를 통한 heap모양을 구축할 수 있다 (트리모양)
#define MAX_ELEMENT 200
typedef struct {
int key;
} element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
} HeapType;
HeapType heap; // 정적 메모리 할당 사용 또는
HeapType *heap = create(); // 동적 메모리 할당 사용heap 삽입 연산
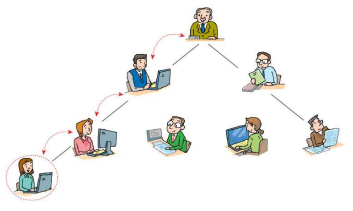
신입이 들어오면 일단 말단 위치에 앉힌 다음에, 승진시키면서
적절한 위치에 유지하게 한다.
heap의 높이가 O(log₂n)이므로, 삽입연산은 O(log₂n)이다.
heap 삭제 연산
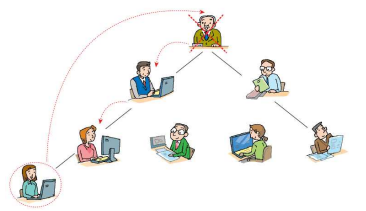
max heap에서의 삭제는 가장 큰 키값을 가진 노드를 삭제하는 것을 의미한다.
-> 따라서 루트노드 삭제
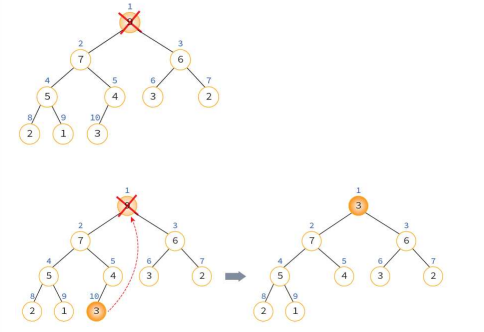
말단 사원을 사장 자리로 올린 다음에, 강등시켜 가며 제자리로 보낸다.
이때 내릴 때 주의해야 할 점은, max이기 때문에
자식 중 큰 값을 찾아서 swap 하며 내려가야 한다.
내려가면서
멈추는 조건은, 자식노드모두보다 크면 멈추면 된다.
또는 가장 말단노드가 된다면 끝.
작은 값이 root자리를 먹게 되면 max heap이 무너지게 때문이다.
heap의 높이가 O(log2n)이므로, 삭제연산은 O(log₂n)이다.
Heap 정렬
하나의 요소를 heap에 삽입하거나 삭제할 때, 시간이 O(log₂n) 만큼 시간이 걸린다.
요소의 개수가 n개이므로 전체적으로 O(nlog₂n)의 시간이 소요한다.
heap 정렬의 가장 좋은 사용처는
가장 큰 값을 항상 좋은 시간복잡도로 뽑을 수 있지만
전체자료가 정렬이 되어있는 것이 아니다 (엉성하게 위의 사진처럼 반만 정렬되어 있는 상태다.)
따라서 가장 큰 값 몇 개만 필요할 때 가장 좋은 성능을 발휘한다.
=> if max heap을 기준으로 말했을 때이다. min heap은 반대이다.
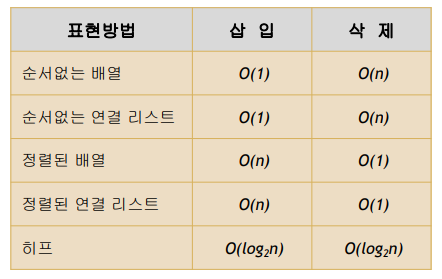
구현하는 방법에 따른 Heap 시간복잡도
'Programming > Data Structure' 카테고리의 다른 글
| [MST] kruskal(크루스칼), prim(프림) 알고리즘 (0) | 2024.02.16 |
|---|---|
| [MST] Prim & Greedy (0) | 2023.09.01 |
우선순위 큐
- 우선순위를 가진 항목들을 저장하는 큐
- 우리가 정한 우선순위대로 정해진 큐

원래라면 1차선 도로처럼 FIFO 순서대로 나아가는 것을 큐(Queue)다.
2차선처럼 우선순위가 높은 데이터가 먼저 나가는 것이 우선순위 큐다.
숫자의 크기를 가지고 일단 우선순위 큐를 만들어보자.
우선순위 큐(heap)은 2가지로 구분
- 최소 우선순위 큐 (min heap)
- 최대 우선순위 큐(max heap)
우선순위 큐 구현방법
3가지가 존재한다

1. 배열을 이용한 우선 순위 큐
| 정렬이 안된 배열 | 정렬이 된 배열 |
삽입 - O(1)
|
삽입 - O(n)
|
연결리스트는 배열과 비슷하다.
3. Heap을 이용한 우선순위 큐
heap이란 무엇인가 하면

이런 뭉텅이를 의미한다.
무슨말이냐면, 정렬이 완전하게 되는 게 아니라
적당히, 이렇게 모여서 모아둔거마냥 반만 정렬되어 있는 상태를 의미한다.
따라서 heap은
노드들이 저장하고 있는 키들이 다음과 같은 식을 만족하는 완전 이진트리(complete binary tree)
1. max heap
부모 노드의 키값이 자식 노드의 키값보다 크거나 같은 완전 이진트리 ( 쉽게 말해, 부모가 큼)

2. min heap
부모 노드의 키값이 자식 노드의 키값보다 작거나 같은 완전 이진트리 ( 쉽게 말해, 부모가 작음)

heap의 높이 log₂n
heap은 구현할 때
배열을 이용하여 구현한다.

배열의 index를 heap의 번호라고 생각한다.
배열로 만들었을 때 장점은
=> 부모노드와 자식노드를 찾기가 쉽다.(관계식이 있기 때문)
- 왼쪽 자식의 인덱스 = (부모의 인덱스)*2
- 오른쪽 자식의 인덱스 = (부모의 인덱스)*2 + 1
- 부모의 인덱스 = (자식의 인덱스)/2
무조건 /2 하면 부모노드의 인덱스를 알 수 있다.
*2 + 1을 하면 오른쪽 자식의 인덱스를 알 수 있다.
이처럼 관계를 통한 heap모양을 구축할 수 있다 (트리모양)
#define MAX_ELEMENT 200
typedef struct {
int key;
} element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
} HeapType;
HeapType heap; // 정적 메모리 할당 사용 또는
HeapType *heap = create(); // 동적 메모리 할당 사용heap 삽입 연산

신입이 들어오면 일단 말단 위치에 앉힌 다음에, 승진시키면서
적절한 위치에 유지하게 한다.
heap의 높이가 O(log₂n)이므로, 삽입연산은 O(log₂n)이다.
heap 삭제 연산

max heap에서의 삭제는 가장 큰 키값을 가진 노드를 삭제하는 것을 의미한다.
-> 따라서 루트노드 삭제

말단 사원을 사장 자리로 올린 다음에, 강등시켜 가며 제자리로 보낸다.
이때 내릴 때 주의해야 할 점은, max이기 때문에
자식 중 큰 값을 찾아서 swap 하며 내려가야 한다.
내려가면서
멈추는 조건은, 자식노드모두보다 크면 멈추면 된다.
또는 가장 말단노드가 된다면 끝.
작은 값이 root자리를 먹게 되면 max heap이 무너지게 때문이다.
heap의 높이가 O(log2n)이므로, 삭제연산은 O(log₂n)이다.
Heap 정렬
하나의 요소를 heap에 삽입하거나 삭제할 때, 시간이 O(log₂n) 만큼 시간이 걸린다.
요소의 개수가 n개이므로 전체적으로 O(nlog₂n)의 시간이 소요한다.
heap 정렬의 가장 좋은 사용처는
가장 큰 값을 항상 좋은 시간복잡도로 뽑을 수 있지만
전체자료가 정렬이 되어있는 것이 아니다 (엉성하게 위의 사진처럼 반만 정렬되어 있는 상태다.)
따라서 가장 큰 값 몇 개만 필요할 때 가장 좋은 성능을 발휘한다.
=> if max heap을 기준으로 말했을 때이다. min heap은 반대이다.
구현하는 방법에 따른 Heap 시간복잡도

'Programming > Data Structure' 카테고리의 다른 글
| [MST] kruskal(크루스칼), prim(프림) 알고리즘 (0) | 2024.02.16 |
|---|---|
| [MST] Prim & Greedy (0) | 2023.09.01 |
