
https://www.acmicpc.net/problem/1749
1749번: 점수따먹기
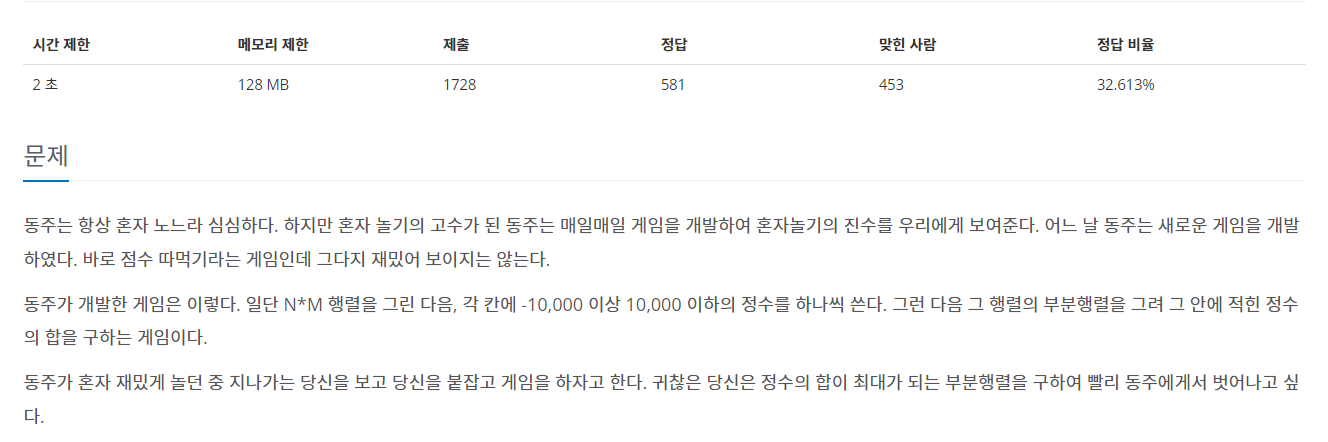
동주는 항상 혼자 노느라 심심하다. 하지만 혼자 놀기의 고수가 된 동주는 매일매일 게임을 개발하여 혼자놀기의 진수를 우리에게 보여준다. 어느 날 동주는 새로운 게임을 개발하였다. 바로 점
www.acmicpc.net
입력
첫째 줄에 N (1 < N < 200), M (1 < M < 200)이 주어진다. 그다음 N개의 줄에 M 개씩 행렬의 원소가 주어진다.
출력
첫째 줄에 최대의 합을 출력하라.
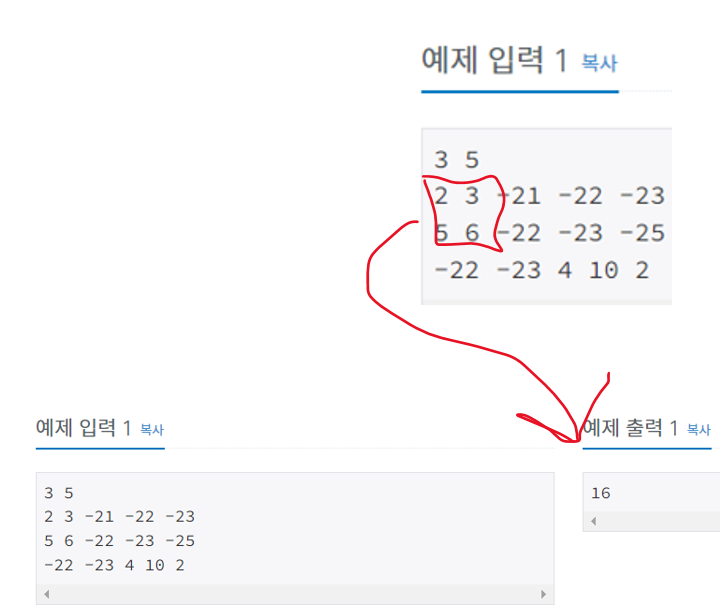
예제 입력1
3 5
2 3 -21 -22 -23
5 6 -22 -23 -25
-22 -23 4 10 2예제 출력 1
16
코드
from sys import stdin
r_line = stdin.readline
h, w = map(int, r_line().split())
matrix = [[0] for _ in range(h)]
for i in range(h): # 높이만큼 반복
matrix[i] = list(map(int, r_line().split()))
prefix_sum = [[0]*(w+1) for _ in range(h+1)]
# 부분합 구하기 (matrix)
for i in range(1, h+1):
for j in range(1, w+1):
prefix_sum[i][j] = (
matrix[i-1][j-1] + prefix_sum[i-1][j] + prefix_sum[i][j-1] - prefix_sum[i-1][j-1]
)
result = float('-inf')
# matix중 부분합을 이용한 최대부분집합 구하기
for i in range(1, h+1):
for j in range(1, w+1):
for k in range(i, h+1):
for l in range(j, w+1):
subarray_sum = (
prefix_sum[k][l] -
prefix_sum[i - 1][l] -
prefix_sum[k][j - 1] +
prefix_sum[i - 1][j - 1]
)
result = max(result, subarray_sum)
print(result)
# print("==============")
# for i in range(1, h+1): # 높이만큼 반복
# for j in range(1, w+1):
# print(prefix_sum[i][j], end=" ")
# print()풀이
위 <그림 1>처럼 부분집합 중 최댓값을 반환하는 게 결과이다.
이때 부분집합을 매번 계산할 수 없기 때문에, 누적합을 이용해야 한다.
2가지를 순서로 풀이를 하면 된다.
일단 첫 번째로 누적합행렬을 만들어야 한다.
예시로,
[1, 2, 3] [1 , 3, 6]
[4, 5, 6] --> [5 , 12, 21]
[7, 8, 9] [12, 27, 45]
왼쪽행렬의 누적합행렬은 오른쪽과 같다.
이를 예시로 누적합을 구하는 풀이를 보면
[1, 3, 6]
[5, 12, 21]
[12, 8, 9] ==> 8의 누적합을 구하는 차례가 됐다고 가정해 보자.

코드를 보고
Prefix_sum[i][j] = 8 + 12 + 12 – 5

이런 식의 결과를 알 수 있다 == 27이다.

예시 그림은 다음과 같다.
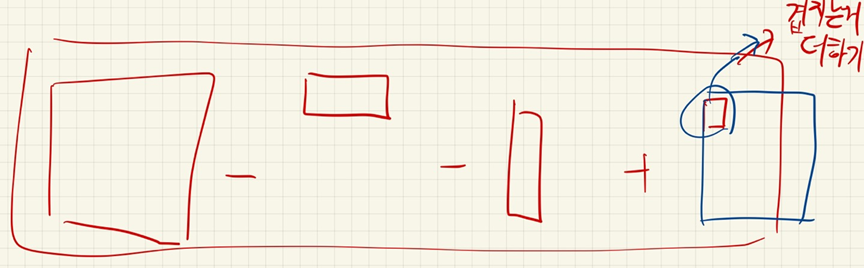
자신자리의 누적합을 구해야 하니, 자신의 숫자, 그리고 현재자신까지의 세로의 누적합, 가로까지의 누적합을 더하고
겹치는 부분 왼쪽 위꼭짓점을 1번 제거한다.
이를 통해 누적합을 구하면 누적합행렬이 나온다.
2번째는 누적합행렬을 통해, 최댓값을 구한다.
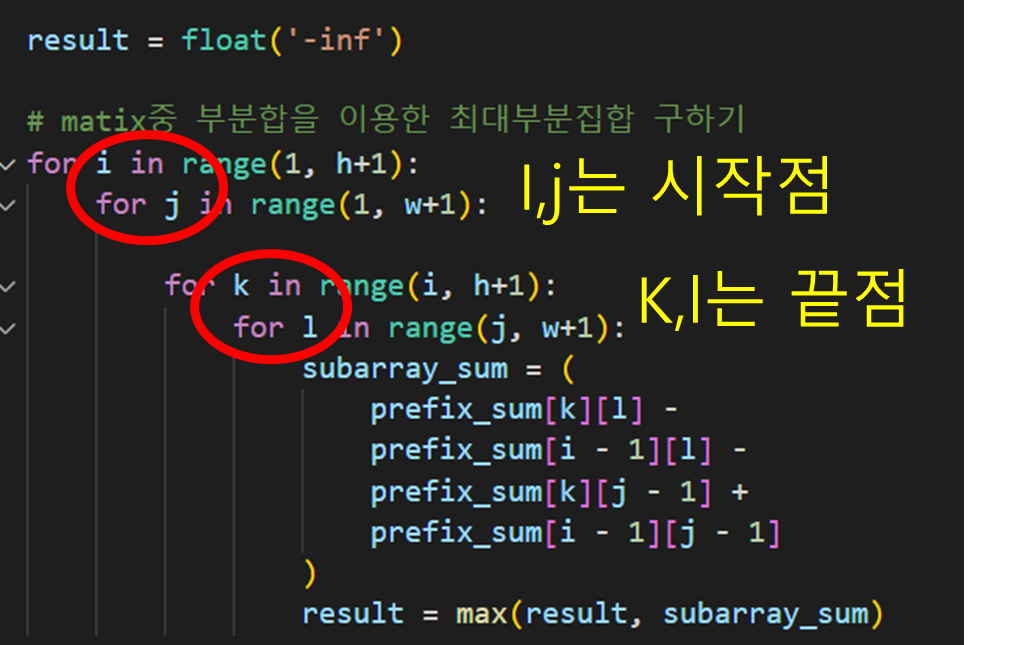
시작점을 기준으로 끝점을 계속 바꿔가며 최대값을 계산한다.
이때 식은 다음과 같다.
그림을 보면
자신의 위치까지의 누적합에서 윗부분, 왼쪽 부분을 제거하고 그중에서 겹치는 부분만 더해서
원하는 모양의 행렬모양을 구한다. 그래서 최댓값을 구한다.
이전 꺼와 비교하여 가장 큰 값을 출력한다.
이때 모든 부분정렬을 검사해야 하므로, 브루트포스의 해당한다.
시간복잡도를 생각해 보면
매트릭스의 최대크기가 h * w이므로, 매트릭스 입력은 O(h * w)의 시간 복잡도를 가집니다.
해보
그다음, 부분집합 최댓값 구하기

번째 반복문은 h번, 두 번째 반복문은 w번 실행되므로, 총 O(h * w)의 시간 복잡도를 가집니다. 내부에 있는 두 개의 반복문은 각각 최대 h와 w번 실행되므로, 총 O(h^2 * w^2)의 시간 복잡도를 가집니다.
하지만
아래의 2개의 for문은 점점 그에 따라 반복수가 줄어들 예정입니다.
따라서 세부적인 시간복잡도는 더 작을 예정이다.

통과를 보면 4.3초에 해당한다.
시간제한은 2초이긴 했다.
python으로 컴파일했을 때는 실패하였다.
pypy3으로 돌렸을 때는 성공하였다.

N (1 < N < 200), M (1 < M < 200)
이 200이 최대이기 때문에 200^200 * 200*200
으로 계산하면 16억이라는 숫자가 나오는데 어찌 통과했는지는 모르겠다.
분석해서 정확한 시간복잡도를 구하고, 다른 방법을 사용할 수 있는지 찾아봐야 할 것 같다.
'Programming > Algorithm(Python)' 카테고리의 다른 글
| [백준/python][stack] 24463번 - 미로 (0) | 2023.10.12 |
|---|---|
| [백준/python][브루트포스] 1018번 - 체스판 다시 칠하기 (0) | 2023.09.02 |
| [백준/python][dp] 백준 13703번 - 물벼룩의 생존확률 (0) | 2023.09.01 |
| [백준/python][브루트포스] 백준 1018번 - 체스판 다시 칠하기 (0) | 2023.09.01 |
| [백준/python][dp] 22968번 - 균형 (0) | 2023.09.01 |
